Was ist der Unterschied zwischen dem Median und dem Mittelwert, bzw. wann sollte der Mittelwert und wann der Median verwendet werden? 

Im Allgemeinen lässt sich der Unterschied zwischen Mittelwert und Median folgendermaßen auf den Punkt bringen:

• Der Mittelwert (Auch bekannt als arithmetisches Mittel oder Durchschnitt) ist prinzipiell die präzisere Kennzahl.
• Auf Grund der höheren Präzision reagiert der Mittelwert empfindlicher gegen Ausreißer oder Messfehler als der Median.
• Der Median ist grundsätzlich unpräziser als der Mittelwert.
• Wenn die untersuchte Stichprobe jedoch mit Ausreißern verunreinigt ist, ist der Median im Vorteil, da er weniger empfindlich gegen Ausreißer ist.
• Die angesprochene Eigenschaft der Präzision wird in statistischer Fachterminologie als "Effizienz" bezeichnet. 
• Die Eigenschaft der Unempfindlichkeit gegen Ausreißer wird in statistischer Fachterminologie als "Robustheit" bezeichnet.
• Somit: Der Mittelwert hat eine hohe Effizienz und eine geringe Robustheit, der Median eine geringe Effizienz aber eine hohe Robustheit.

Betrachten wir nun ein Beispiel um das Verhalten von Mittelwert und Median in unterschiedlichen Situationen zu analysieren. Wir untersuchen hierbei zunächst, wie sich Mittelwert und Median bei Vorliegen einer Normalverteilung verhalten. 

Hierzu haben wir an einem regnerischen Tag 200 Regenwürmer gesammelt, die Körperlänge jedes Regenwurms gemessen und daraufhin den Mittelwert und den Median der Regenwurmlängen berechnet. In der nachfolgenden Abbildung ist das Histogramm der Regenwurmlängen zusammen mit deren Mittelwert und Median dargestellt:

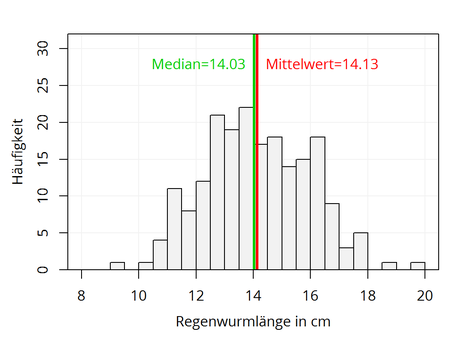
Sie erkennen, dass für diese Stichprobe der Median und der Mittelwert nahezu gleich sind: Der Median beträgt hier 14.03 cm und der Mittelwert 14.13 cm. Der Grund dafür, warum Median und Mittelwert hier fast gleich sind, ist dass diese Verteilung symmetrisch ist und keine Ausreißer vorliegen. Im Falle einer symmetrischen Verteilung, die frei von Ausreißern ist, zeigen Median und Mittelwert somit nahezu keinen Unterschied.

Betrachten wir nun ein weiteres Beispiel: Hier wurden 200 Personen nach Ihrem monatlichen Einkommen befragt und erneut der Mittelwert und der Median des Einkommens berechnet. Der Mittelwert und der Median sind zusammen mit dem Histogramm der Einkommen in der nächsten Abbildung dargestellt. 

Man erkennt in dieser Abbildung Folgendes: Die Verteilung der Einkommen ist deutlich rechtsschief. D.h. es gibt viele Personen mit einem "normalen" Monatseinkommen von bis zu 5000 € und einige wenige Personen mit einem sehr hohen Monatseinkommen von z.B. 20000 € und mehr. Der Median des Einkommens beträgt hier 2989 €, während das arithmetische Mittel mit einem Wert von 4106 € wesentlich höher liegt. Das arithmetische Mittel ist hier deutlich höher als der Median, da die Variable Einkommen eine rechtsschiefe Verteilung hat.

Falls Sie also eine schiefe Verteilung untersuchen, ist davon auszugehen dass Median und Mittelwert unterschiedliche Werte liefern. Im Allgemeinen wird bei einer Schiefen Verteilung (Wie z.B. die Verteilung des Monatseinkommens) der Median bevorzugt, da der Median eine realistischere Einschätzung der Verteilung ermöglicht.

Fazit: Falls Sie also eine rechtsschiefe, oder eine linksschiefe Variable analysieren, dann geben Sie zusätzlich zum arithmetischen Mittel immer den Median an! In der Praxis kommen insbesondere rechtsschiefe Variablen häufig vor, und bei einer rechtsschiefen Variable ist der Mittelwert in der Regel deutlich größer als der Median. 

Sie haben weitere Fragen zum Thema Mittelwert vs. Median? Buchen Sie eine statistische Beratung und stellen Sie uns Ihre Fragen!