Die Varianzhomogenität ist Voraussetzung für zahlreiche statistische Verfahren, wie z.B. den t-Test für unabhängige Stichproben. Im Vorfeld solcher Verfahren ist es ratsam, zunächst zu überprüfen ob die Varianzhomogenität für die zu untersuchenden Daten gegeben ist. Eine Methode hierzu sind Tests auf Varianzhomogenität.

Beginnen wir zunächst mit einer graphischen Definition des Begriffes der Varianzhomogenität. Die nachfolgende Graphik stellt zwei varianzhomogene Variablen A und B dar:

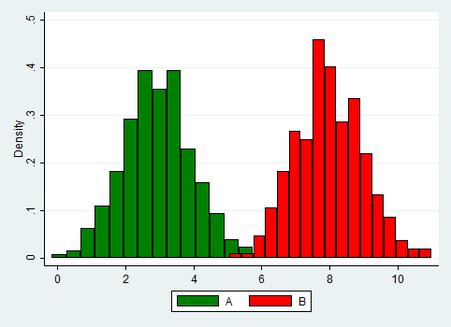
Die Varianzhomogenität besagt, dass die Streuung in den beiden Gruppen gleich hoch ist. Dies ist in obiger Graphik offensichtlich der Fall, denn die die Histogramme der Gruppen A und B sind in etwas gleich "breit", zeigen also eine ähnliche Streuung.

Betrachten wir im Gegensatz dazu eine analoge Graphik für zwei nicht varianzhomogene Variablen C und D:

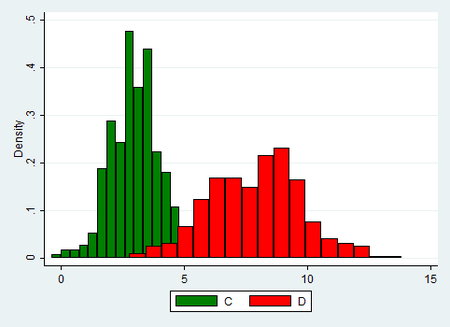
Man erkennt, dass in dieser Graphik die Streuungen in den beiden Gruppen sehr unterschiedlich sind: Das rote Histogramm der Gruppe D weist eine deutlich höhere Streuung auf als dasjenige der Gruppe C.

Wie so häufig in der statistischen Beratung kann man auch hier untersuchen ob der beobachtete Unterschied in den Streuungen statistisch signifikant ist, wozu ein Signifikanztest auf Varianzhomogenität verwendet wird. In Stata ist hierfür der Befehl sdtest verfügbar.  

Wie wenden den Befehl sdtest in Stata nun zunächst auf die beiden Gruppen A und B an, und erhalten folgenden Output:

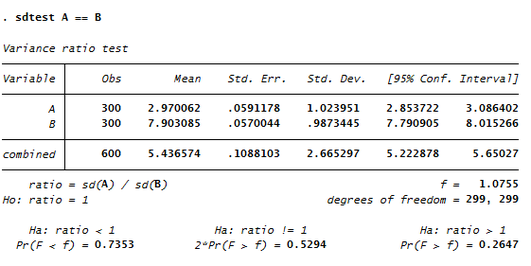
Wir konzentrieren uns auf die wichtigsten Kennzahlen des Outputs. Im oberen Teil der Tabelle sind in der Spalte Std. Dev. die Standardabweichungen der Daten dargestellt. Die Standardabweichung der Gruppe A beträgt 1.0239, diejenige der Gruppe B beträgt 0.9873. Der unterschied zwischen den beiden Werten fällt also ziemlich klein aus, und deutet auf eine vorliegende Varianzhomogenität hin.

Ebenfalls finden wir im Output ganz unten in der Mitte den p-Wert des Tests. Dieser beträgt p=0.5294 und ist damit deutlich größer als das allgemein übliche Signifikanznveau von 0.05. Somit besagt das Testergebnis, dass bei den beiden Gruppen A und B von Varianzhomogenität ausgegangen werden kann.

Sie möchten weitere Artikel zum Thema Stata oder Statistik lesen? Hier geht es zurück zur Artikel-Übersicht.

Informationen über unser Angebot der statistischen Beratung finden Sie hier: Unterstützung Datenanalyse.