In diesem Tutorial erklären wir Ihnen, wie Sie Zufallszahlen aus verschiedenen statistischen Verteilungen in Stata simulieren. Künstlich erzeugte Zufallszahlen Spielen in der Statistik Beratung eine wichtige Rolle und werden häufig benutzt um Analysemethoden auszuprobieren oder zu kalibrieren.

Um unsere Zufallszahlen generieren und abspeichern zu können, beginnen wir mit einem leeren Datensatz mit 500 Zeilen. Hierzu geben Sie die folgenden Befehle ein:

clear

set obs 500

Der erste Befehl erzeugt ein leeres Datenblatt und der zweite Befehl setzt die Anzahl der Zeilen auf 500. Betrachten wir nun die wohl bekannteste Verteilung, nämlich die Normalverteilung.

Die Normalverteilung besitzt die Parameter µ und σ. Hierbei ist µ der Erwartungswert und σ die Standardabweichung der Verteilung. Eine Normalverteilung mit µ=0 und σ=1 wird als Standardnormalverteilung bezeichnet. 

Wir möchten nun 500 Zufallszahlen aus einer Standardnormalverteilung generieren. Hierzu geben wir folgenden Befehl in Stata ein:

generate X = rnormal(0,1) 

Durch den Befehl rnormal(0,1) fordern wir Zufallszahlen aus einer Standardnormalverteilung an. Man kann anstatt von 0 und 1 jedoch auch andere Werte für Erwartungswert und Standardabweichung auswählen.

Im Datensatz erscheint nun eine neue Variable X, die standardnormalverteilte Zufallszahlen enthält. Sehen Sie sich nun die Verteilung der Variable X an, indem Sie ein Histogramm erstellen. Benutzen Sie dazu das folgende Kommando:

histogram X 

Sie erhalten sodann ein Schaubild, das ungefähr folgendermaßen aussieht:

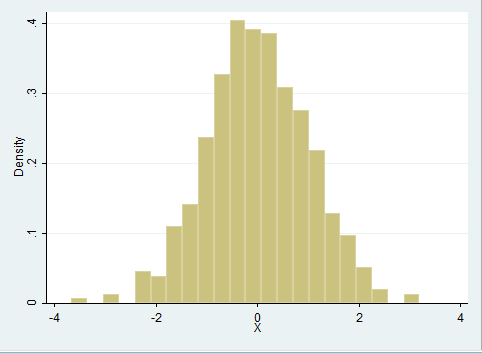
Man erkennt in der Struktur der Zufallszahlen gut die Form der Dichte der Normalverteilung (Glockenkurve) wieder. Des weiteren erkennt man, dass die Zahlen symmetrisch um den Wert 0 streuen. Außerdem ist sichtbar, dass ein Großteil der Werte zwischen -1.96 und +1.96 liegt. In diesem Bereich liegt bei einer Standardnormalverteilung in der Regel 95% aller Werte.

Nun erzeugen wir weitere normalverteilte Zufallszahlen, wobei wir andere Zahlen für µ und σ wählen, nämlich einerseits µ=3, σ=1 andererseits µ=8, σ=2. 

Die so erzeugten Zufallszahlen werden dann wieder gemeinsam in einem Histogramm dargestellt. Geben Sie hierzu folgenden Code ein:

generate X2 = rnormal(3,1)

generate X3 = rnormal(8,2)

graph twoway (histogram X2, fcolor("blue")) ///

(histogram X3, fcolor("red")), legend(lab(1 "X2") lab(2 "X3"))

Sie erhalten sodann das folgende Schaubild:

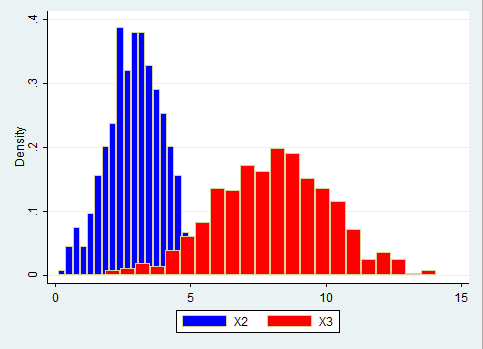
Man erkennt in diesem Schaubild verschiedene Charakteristika der Normalverteilung. Das blaue Histogramm zentriert sich um die Zahl 3, da zuvor 3 als Erwartungswert gewählt wurde. Das rote Histogramm ist dementsprechend symmetrisch um den Wert 8.

Weiterhin wird sieht man, dass das blaue Histogramm deutlich schmaler und höher ist als das rote, da X2 die Standardabweichung zu 1, bei X3 hingegen zu 2 gewählt wurde, weshalb X3 eine deutlich größere Streuung aufweist.

Lassen Sie uns nun eine weitere Verteilung auswählen und graphisch darstellen, wie z.B. die Poisson-Verteilung.

Zur Generierung von Poisson-verteilten Zufallszahlen wird der Befehl rpoisson verwendet:

generate X4 = rpoisson(14)

generate X5 = rpoisson(25)

graph twoway (histogram X4, fcolor("blue")) (histogram X5, fcolor("red")), legend(lab(1 "X4") lab(2 "X5"))

Man erhält durch diese Eingabe das folgende Schaubild:

Sie möchten weitere Artikel zum Thema Stata oder Statistik lesen? Hier geht es zurück zur Artikel-Übersicht. 

Falls Sie sich für eine Statistik-Beratung zum Thema Stata interessieren, nehmen Sie Kontakt uns auf und vereinbaren einen persönlichen Termin.