Der Mann-Whitney-U-Test wird allgemein als nichtparametrische Alternative zum t-Test für unabhängige Stichproben angesehen. Er wird zumeist angewandt, wenn die Voraussetzungen des t-Tests nicht gegeben sind. Eine andere Bezeichnung für den Mann-Whitney-U-Test ist Wilcoxon-Rangsummen-Test.

Erinnern wir uns zunächst an den t-Test für unabhängige Stichproben. Dieser hat die folgenden Voraussetzungen:

1. Metrisches Messniveau der betrachteten Variablen
2. Normalverteilung in beiden Gruppen
3. Gleiche Varianz in beiden Gruppen

Der Mann-Whitney-U-Test wird angewandt, wenn entweder die 1. Voraussetzung (metrisches Messniveau) oder die 2. Voraussetzung (Normalverteilung) nicht gegeben ist. 

Wenn hingegen nur die 3.Voraussetzung (Gleichheit der Varianz) nicht erfüllt ist, kann der t-Test dennoch berechnet werden wobei jedoch die Welch-Korrektur für ungleiche Varianzen benutzt werden muss.

Betrachten wir nun das folgende Beispiel zum Mann-Whitney-U-Test: Wir interessieren uns, ob Rauchen einen Einfluss auf den Cholesteringehalt des Blutes hat und haben hierzu jeweils 30 Raucher und Nichtraucher rekrutiert. Von jeder Person wurde eine Blutprobe genommen, und die Konzentration des Cholesterins in mikrogramm pro cl Blut gemessen. Die Ergebnisse können Sie hier als .txt-Datei herunterladen:

Nach dem Herunterladen befindet sich der Datensatz in ihrem Downloads-Ordner. Lesen Sie die Datensatz in Stata ein, indem Sie den folgenden Code eingeben:

insheet using "C:\Users\Jakob\Downloads\Chol.txt" , clear

Ersetzen Sie hierbei den Usernamen Jakob durch den Usernamen den Sie auf Ihrem Rechner verwenden. 

Öffnen Sie nun den Dateneditor. Geben Sie hierzu den folgenden befehl ein:

edit

Sie erkennen nun im Dateneditor, dass der Datensatz folgende Gestalt hat:

Neben einer Probanden-ID-Nummer enthält der Datensatz die Variable smoke, die angibt ob ein Proband Raucher (smoke=1) oder Nichtraucher (smoke=0). Die Variable chol enthält den gemessenen Cholesterin-Wert.

Wir überprüfen nun zunächst, ob es möglich ist die beiden Gruppen mit einem t-Test für unabhängige Stichproben zu untersuchen. Um zu untersuchen ob die Daten in beiden Gruppen normalverteilt sind, erstellen wir getrennt für jede Gruppe ein Histogramm der Daten. Zusätzlich wird in beide Histogramme eine Kurve der Dichte der Normalverteilung eingezeichnet. Dazu wird folgender Stata-Befehl verwendet:

histogram chol, by(smoke) normal

Wir erhalten im Ergebnis das folgende Schaubild:

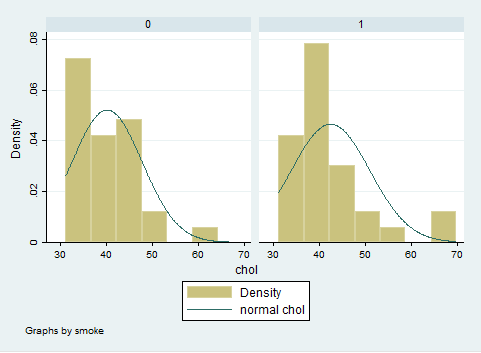
Es ist deutlich erkennbar, dass die Normalverteilung die Cholesterin-Werte nicht gut mit der Normalverteilungskurve übereinstimmen. Die Verteilung der Cholesterin-Werte ist offensichtlich nicht symmetrisch und rechtsschief, d.h. es gibt einige deutliche Abweichungen von der Mitte aus gesehen nach rechts.  

An dieser Stelle wird also entschieden, dass die Daten nicht für den t-Test geeignet sind, da die Voraussetzung der Normalverteilung nicht erfüllt ist.

Wir führen nun denn Mann-Whitney-U-Test durch und geben hierzu den folgenden Stata-Befehl ein:

ranksum chol, by(smoke)

Der Output des Befehls sieht folgendermaßen aus:

Betrachten Sie zunächst den p-Wert der Tests. Sie finden Ihn ganz unten. Der p-Wert beträgt p=0.2739. Da der Wert größer ist als 0.05, liegt zwischen Rauchern und Nichtrauchern kein signifikanter Unterschied vor.

Weiterhin sind wir daran interessiert herauszufinden, welche Gruppe tendenziell die größeren Cholesterin-Werte aufweist, auch wenn dieser Unterschied statistisch nicht signifikant ist.

Hierzu betrachten wir die Ransummen (rank sum). Es wird deutlich, dass die Gruppe der Raucher (smoke = 1) eine höhere Rangsumme aufweist. Somit haben Raucher tendenziell höhere Cholesterin-Werte.

Sie möchten weitere Artikel zum Thema Stata oder Statistik lesen? Hier geht es zurück zur Artikel-Übersicht. Informationen über unser Angebot der Stata-Nachhilfe finden Sie hier: Stata-Nachhilfe.