Der Chi-Quadrat Test in SPSS ist einer der bekanntesten und am häufigsten eingesetzten Signifikanztests. Er dient zur Analyse von Zusammenhängen zwischen zwei qualititativen Variablen. In diesem Artikel demonstrieren wir Ihnen anhand eines Beispieldatensatzes das Folgende:

• Die Berechnung des Chi-Quadrat-Unabhängigkeitstests mit SPSS
• Erstellung von zweidimensionalen Kreuztabellen in SPSS
• Interpretation der Ergebnisse des Chi-Quadrat-Tests in SPSS
• Tipps zum Berichten der Testergebnisse

Betrachten wir nun zunächst unseren Beispieldatensatz. Dieser ist in folgendem SPSS-Screenshot dargestellt:

Der Datensatz enthält Information über insgesamt 100 Personen, die an einer Befragung teilgenommen haben.

Die Variable Partei enthält die bevorzugte Partei der Personen. Die Befragten konnten hierbei wählen, welche der drei Parteien SPD, CDU und Grüne am meisten Ihrer Präferenz entspricht. Weiterhin enthält der Datensatz das Geschlecht der Person.

Wir möchten nun untersuchen, ob einen Zusammenhang zwischen Geschlecht und Parteipräferenz gibt, d.h. ob z.B. eine bestimmte Partei von Männern oder Frauen bevorzugt wird. Da sowohl das Geschlecht als auch die bevorzugte Partei eine kategorielle Variable ist, ist der Chi-Quadrat-Test das geeignete Analyseverfahren.

Um den Test durchzuführen, wählen wir in SPSS den Menüpfad Analysieren -> Deskriptive Statistik -> Kreuztabellen. In diesem Menü muss nun eine der Variablen bei Zeilen und die andere bei Spalten eingefügt werden. Welche der Variablen wo eingefügt wird ist hierbei egal.

Dieser Schritt ist in folgender Abbildung dargestellt:

Nun müssen Sie noch links auf den Button Statistiken klicken. Es öffnet sich daraufhin ein weiteres Menü mit der Überschrift Kreuztabellen: Statistik. In diesem Menü müssen Sie nun links oben einen Haken bei Chi-Quadrat setzen, wie in nachfolgender Abbildung dargestellt ist:

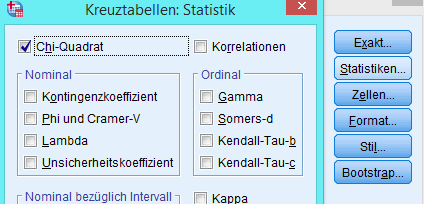
Drücken Sie anschließend auf Weiter und dann auf OK. Sie erhalten nun im SPSS Output-Fenster den Output des Chi-Quadrat-Tests:

 
Betrachten Sie zunächst die Tabelle mit der Überschrift Partei * Geschlecht. Dies ist eine Kreuztabelle, die eine deskriptive Einschätzung des Zusammenhangs zwischen Geschlecht und Parteipräferenz erlaubt. Man erkennt, dass die CDU von 23 Männern bevorzugt wird, jedoch nur von 11 Frauen. Die SPD hingegen wird eher von Frauen bevorzugt (25 Frauen gegenüber 15 Männern).
Somit deuten die Ergebnisse der Kreuztabelle darauf hin, dass ein Zusammenhang zwischen den beiden Variablen vorliegt.

Betrachten Sie nun die Tabelle mit der Überschrift Chi-Square Tests. Diese Tabelle enthält das Ergebnis des Chi-Quadrat-Tests, welcher eine Einschätzung darüber liefert oder der Zusammenhang zwischen Geschlecht und Parteipräferenz statistisch signifikant ist.

Die wichtigste Kennzahl in diesem Output ist der p-Wert. Dieser ist in der Spalte Asymptotic Significance (2-sided) dargestellt. Der p-Wert des Tests hat hier den Wert p=0.032 und ist somit kleiner als 0.05, das bedeutet dass der Zusammenhang zwischen Geschlecht und Partei signifikant ist.

Um das Ergebnis des Chi-Qadrat-Tests in einer Ausarbeitung zu berichten, benötigen Sie zusätzlich noch den Chi-Quadrat-Wert (in der Spalte Value) und die Freiheitsgrade (in der Spalte df). Der Value beträgt hier 6.889 und die df haben den Wert 2. Mit diesen beiden Zahlen sowie dem p-Wert können Sie das Ergebnis des Tests folgendermaßen berichten:

Der  χ²-Test resultiert in einem Ergebnis von χ²(2)=6.889, p = 0.032.

Beachten Sie weiterhin noch die folgenden Anmerkungen zur Berechnung von Kreuztabellen und Chi-Quadrat-Tests in SPSS.

• Wenn Sie sich nur für die Häufigkeitsverteilung einer einzelnen kategoriellen Variable, und nicht für den Zusammenhang zwischen zwei Variablen interessieren, dann sollten Sie anstatt der Kreuztabelle eine einfache Häufigkeitstabelle mit SPSS erstellen.
• Wenn Sie möchten, dass in Ihrer SPSS-Kreuztabelle Prozente bzw. prozentuale Häufigkeiten angezeigt werden, dann gehen Sie wieder in das Menü Analysieren -> deskriptive Statistiken -> Kreuztabellen und klicken Sie auf den Button Zellen. Hier haben Sie bei Prozentwerte (Links in der Mitte) die Auswahl zwischen Zeilenweise, Spaltenweise und Gesamtsumme.
• Wenn Sie Zeilenweise auswählen, erhalten Sie Prozentzahlen, die sich in jeder Zeile zu 100% aufaddieren (Analog für Spaltenweise). Wenn Sie Gesamtsumme auswählen, erhalten Sie Prozentzahlen die sich auf die gesamte Tabelle beziehen.
• Weiterhin ist zu beachten, dass der Chi-Quadrat-Test in SPSS eine Voraussetzung hat, nämlich dass die sogenannten erwarteten Häufigkeiten der Kreuztabelle sämtlich größer als 5 sind.
• Prinzipiell können Sie eine Kreuztabelle auf Variablen mit beliebigem Messniveau (qualitativ, ordinal oder metrisch) anwenden. Allerdings ist es in der Praxis unüblich, Kreuztabellen für metrische oder ordinale Variablen zu berechnen. Zur Analyse von Zusammenhängen von metrischen / ordinalen Variablen ist die Korrelationsanalyse in SPSS besser geeignet.
• Kreuztabellen werden schnell unübersichtlich, wenn Sie für Variablen mit großer Anzahl an Ausprägungen berechnet werden. Nehme Sie als Faustregel, dass eine Kreuztabelle nicht mehr als ca. 30 Zellen haben sollte (Das entspricht einer Tabelle für 2 Variablen von denen eine 5 und eine 6 Ausprägungen hat).
• Wenn in Ihrer Analyse eine größere Tabelle resultieren würde, können Sie einige Ausprägungen Variablen zu Kategorien zusammenfassen.