Die robuste Statistik ist ein Teilgebiet, das sich mit Methoden beschäftigt, welche auch dann noch gute Ergebnisse liefern wenn die betrachteten Daten mit Ausreißern oder Messfehlern verunreinigt sind. Ein klassisches Beispiel ist die deskriptive Beschreibung von Einkommen.

Nehmen wir z.B. an, es liege uns in einem Statistik-Beratungs-Projekt der folgende Datensatz des jährlichen Einkommens von 8 zufällig ausgewählten Personen vor:  

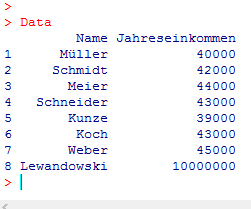
Man erkennt, dass die Gehälter der ersten 7 Personen im Bereich von 39000 € bis 45000 € liegen, während die letzte Person ein sehr hohes Jahresgehalt von € 10000000 bezieht.

Wir interessieren uns nun für das durchschnittliche Einkommen und berechnen daher mit R den Durchschnitt der Jahresgehälter:

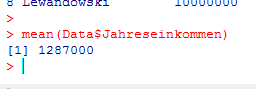
Das mittlere Jahresgehalt in diesem Datensatz beträgt 1287000 €, also etwas über eine Million €. Zwar haben wir den Mittelwert korrekt berechnet, aber das Durchschnittsgehalt von 1287000 € beschreibt den Datensatz nur sehr schlecht, da die allermeisten Personen sehr viel weniger verdienen. 

Diese Situation ist ein Beispiel dafür, dass Ausreißer oder Messfehler ein statistisches Ergebnis sehr stark beeinflussen oder verfälschen können, wenn nicht-robuste Analysemethoden benutzt werden. Daher führen wir die Analyse noch einmal durch und benutzen diesmal anstatt des Durchschnitts den Median: 

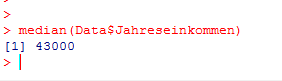
Das mediane Einkommen ergibt sich zu 43000 €. Diese Zahl vermittelt dem Leser eine sehr viel bessere Vorstellung von der Beschaffenheit der Daten, da die allermeisten Personen nicht viel mehr oder weniger als 43000 € verdienen. 

In Datensituationen, in denen das Vorliegen von Ausreißern nicht ausgeschlossen werden kann, sind robuste Methoden somit den klassischen Methoden vorzuziehen.

Betrachten wir nun als weiteres Beispiel die Regressionsanalyse. Nehmen wir an, es liegen zwei Variablen X und Y vor, wobei Y die abhängige und X die unabhängige Variable ist. 

Das Streudiagramm der beiden Variablen sieht folgendermaßen aus:

Man erkennt, dass zwischen X und Y ein guter linearer Zusammenhang besteht, so dass es sinnvoll erscheint, eine lineare Regression zu berechnen. Allerdings sind auch einige Ausreißer enthalten (rot markiert). Wir berechnen nun eine gewöhnliche lineare Regression (ordinary least squares bzw. OLS) für diese Daten und erhalten folgende Regressionsgerade:

Es wird deutlich, dass die Ausreißer einen starken Effekt auf das Ergebnis haben. Die Regressionsgerade wird deutlich in Richtung der rot markierten Ausreißer gezogen, wodurch die Regression den Verlauf der grauen Punkte nur unbefriedigend wiedergibt.

Als Alternative zur gewöhnlichen linearen Regression versuchen wir nun eine robuste Regressionsmethode. In R sind mehrere solcher Methoden implementiert. Wir wählen die Funktion rlm() aus dem Paket MASS. Diese Funktion berechnet einen sogenannten M-Schätzer unter Verwendung des IWLS-Algorithmus (iterated re-weighted least squares).

Die so berechnete robuste Regressionsgerade wird zusätzlich in das Schaubild eingetragen:

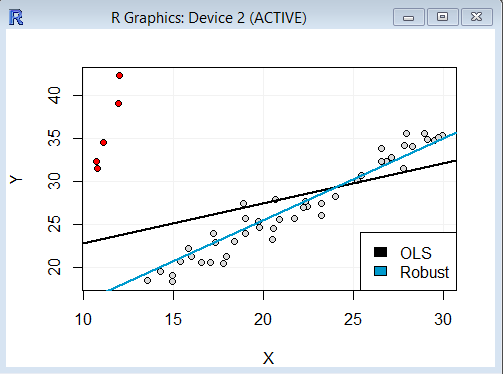
Es wird deutlich, dass die blau markierte robuste Regressionsgerade klar den Verlauf der Mehrheit der Datenpunkte wiedergibt und von den Ausreißern kaum beeinflusst wird.

Sie möchten weitere Artikel zum Thema R oder Statistik lesen? Hier geht es zurück zur R-Artikel-Übersicht.

Falls Sie sich für eine Statistik-Beratung zum Thema R interessieren, nehmen Sie Kontakt uns auf und vereinbaren einen persönlichen Termin.