Nichtparametrische Verfahren sind statistische Verfahren, die keine oder nur sehr geringe Voraussetzungen an die Verteilung der untersuchten Daten stellen. Die bekanntesten nichtparametrischen Tests sind der Wilcoxon-Test und der Mann-Whitney-U-Test. Im folgenden finden Sie eine Anleitung zur Durchführung der Tests und Interpretation der Ergebnisse in R.

Die im folgenden erläuterten nichtparametrischen Verfahren sollten Sie immer dann einsetzen, wenn die Voraussetzungen für einen t-Test nicht gegeben sind. Es kommen hierbei zwei Szenarien in Frage:

• Wenn sie einen t-Test für verbundene Stichproben durchführen möchten, die Voraussetzung aber nicht gegeben sind, dann verwenden Sie den Wilcoxon-Test.
• Wenn sie einen t-Test für unabhängige Stichproben durchführen möchten, die Voraussetzung aber nicht gegeben sind, dann verwenden Sie den Mann-Whitney-U-Test.

Achtung: der Mann-Whitney-U-Test wird vereinzelt auch als Wilcoxon-Test bezeichnet, jedoch als Wilcoxon-Test für unabhängige Stichproben.

Wir führen den Test an einem Beispiel-Datensatz mit Namen calcium durch. Dieser Datensatz enthält für 100 Patienten jeweils eine Vorher- und eine Nachher-Messung des Calcium-Gehaltes der Knochen. Zwischen den beiden Messungen erfolgte eine Therapie, die zum Ziel hatte den Calciumgehalt zu erhöhen. Der Datensatz hat die folgende Gestalt:

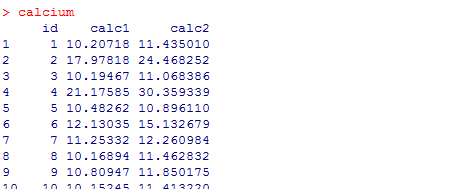
Zur Durchführung des Wilcoxon-Tests verwenden wir die Funktion wilcox.test(). Wir geben den Befehl

wilcox.test(calcium$calc1,calcium$calc2,paired=TRUE)

ein. Der Schreibweise calcium$calc1 bedeutet, dass wir auf die Variable calc1 aus dem Datensatz calcium zugreifen möchten (Analog für calc2). Die Option paired=TRUE wird benötigt, da es sich bei einem Vorher-Nachher-Design verbundene Stichproben handelt.

Wir erhalten nach der Eingabe des Befehls den folgenden Output:

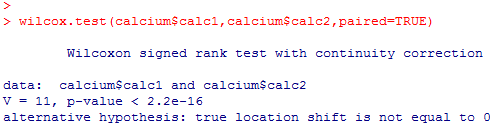
Der Output enthält als wichtigste Kennzahl den p-Wert. Dieser wird als p < 2.2e-16 angezeigt. Das bedeutet, der p-Wert ist praktisch Null, denn die Zahl 2.2e-16 ist die wissenschaftliche Schreibweise für die Zahl 0.00000000000000022. Da der p-Wert deutlich kleiner ist als 0.05, liegt hier ein hochsignifikanter Unterschied zwischen den beiden Messungen des Calcium-Gehaltes vor.

Ihr Statistik-Berater weist Sie jedoch noch auf folgendes hin: Dieses Ergebnis gibt Ihnen noch keinen Aufschluss darüber, ob die Vorher- oder die Nachher-Messung einen höheren Calcium-Gehalt aufweist. Wir empfehlen Ihnen daher, zusätzlich noch z.B. die Mittelwerte der beiden Messungen zu berechnen. Dies können Sie folgendermaßen machen:

mean(calcium$calc1)

mean(calcium$calc2)

Sie erhalten dann das folgende Ergebnis:

Die zweite Messung weist einen größeren Mittelwert auf als die erste. Somit zeigt die Behandlung die gewünschte Wirkung.

Betrachten wir nun den Mann-Whitney-U-Test in R. Dies ist ein nichtparametrischer Test zum Vergleich zweier unabhängiger Stichproben.

Um den Mann-Whitney-U-Test anwenden zu können, benötigen Sie zwei unabhängige Stichproben, wie zum Beispiel Männer und Frauen oder Behandlungs- und Kontrollgruppe.

Wir führen das obige Beispiel fort und Betrachten nun folgende Situation: Eine Gruppe von Personen hat das Medikament erhalten und eine andere Gruppe hat ein Placebo erhalten. Bei beiden Gruppen wird sodann das Calcium gemessen. Der resultierende Datensatz hat in diesem Beispiel die Bezeichnung calcium2 und weist folgende Gestalt auf:

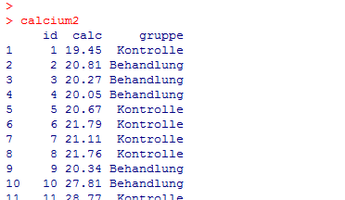
Die Variable calc enthält wie im letzten Beispiel den gemessenen Calciumgehalt, während die Variable gruppe angibt, ob der jeweilige Patient zur Kontroll- oder zur Behandlungsgruppe gehört.

Um in R den Mann-Whitney-U-Test zu berechnen, verwenden wir wieder die Funktion wilcox.test(), die diesmal jedoch auf andere Art eingesetzt werden muss. Geben Sie zur Berechnung des Tests den folgenden befehl ein:

wilcox.test(calcium2$calc ~ calcium2$gruppe) 

Innerhalb des Befehls wilcox.test() wird zunächst die Variable angegeben, die analysiert werden soll, danach muss eine Tilde ~ eingegeben werden und zum Schluss die Variable, welche die Gruppenzugehörigkeit angibt, in unserem Fall ist das gruppe. Sie erhalten dadurch den folgenden Output:

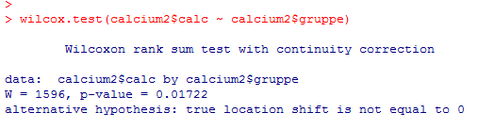
Die wichtigste Kennzahl ist hier der p-Wert, der im Output unter p-value aufgelistet ist. Der p-Wert beträgt hier p=0.01722. Da dieser Wert kleiner ist als 0.05, liegt zwischen Kontroll- und Behandlungsgruppe ein signifikanter Unterschied hinsichtlich der Calciumkonzentration der Knochen auf.

Beachten Sie: Dieses  Ergebnis erlaubt Ihnen noch keine Entscheidung darüber, welche Gruppe durchschnittlich die höhere Calcium-Konzentration aufweist. Um dies in Erfahrung zu bringen, berechnen Sie den Mittelwert der Calciumkonzentration getrennt für beide Gruppen.

Hierzu können Sie z.B. die praktische R-Funktion tapply verwenden. Geben Sie den folgenden R-Code ein:

tapply(calcium2$calc,calcium2$gruppe,mean)

Die R-Funktion tapply funktioniert folgendermaßen:

• Das erste Argument calcium2$calc, das innerhalb der Funktion tapply angegeben wurde, ist die Funktion von der wir Mittelwerte berechnen möchten.
• Als zweites Argument geben wird die Gruppierungsvariable an, in unserem Fall calcium2$gruppe.
• Das dritte Argument mean ist die Funktion, die wir anwenden möchten. Dies ist hier die Funktion mean, da wir getrennt-
• Die Funktion tapply wendet dann die Funktion mean auf die Daten calcium2$calc an, und zwar für jede der Gruppen die durch  calcium2$gruppe festgelegt werden.

Die Anwendung der Funktion tapply auf die eben beschriebene Weise resultiert in folgendem Output in der R-Konsole:

Man erkennt unschwer, dass die Behandlungsgruppe eine höhere Calcium-Konzentration aufweist als die Kontrollgruppe. Somit konnte für das Medikament die Wirksamkeit nachgewiesen werden. 

Möchten Sie den Wilcoxon-Test sowie den Mann-Whitney-U-Test mit R-Studio lieber in Form eines Video-Tutorials erlernen? Sehen Sie sich in diesem Fall die folgenden beiden Videos auf Youtube an.

Wenn Ihnen die Videos gefallen, würden wir und freuen wenn Sie unseren Kanal abonnieren würden!