Tests auf Normalverteilung in R
Hier lernen Sie, mit welchen Tests eine Normalverteilung in R geprüft werden kann und wie man dies in R vornimmt. Aus Grund der großen Bedeutung der Normalverteilung wurden im Laufe der Zeit zahlreiche Tests entwickelt, um das Vorliegen dieser Verteilung überprüfen zu können. Die bekanntesten in R verfügbaren Tests auf Normalverteilung sind die folgenden:
- Shapiro-Wilk-Test in R: Dies ist der wohl gängigste Test auf Normalverteilung. Im Allgemeinen wird dem Test nachgesagt, eine hohe Teststärke zu haben, worin der Grund für seine Popularität liegt
- Kolmogorov-Smirnov-Test in R: Dieser Test besitzt zwar auch eine hohe Bekanntheit, aber er gilt zur Prüfung einer Normalverteilung als weniger teststark und wird daher eher seltener angewandt.
- Es existieren in R noch weitere Tests auf Normalverteilung, die jedoch weniger bekannt sind. Beispiele sind der Anderson-Darling-Test in R und der Jarque-Bera-Test.
Im Folgenden zeigen wir Ihnen, wie man den Shapiro-Wilk-Test und den Kolmogorov-Smirnov-Test in R durchführt.
In R Normalverteilung prüfen / Tests auf Normalverteilung in R
Um die Normalverteilungstests in R zu demonstieren, benötigen wir zunächst ein paar Daten. Wir nutzen hierzu die Möglichkeit zur Erzeugung von Zufallszahlen in R, und erstellen uns zwei Stichproben:
- Vor dem Erzeugen der Zufallszahlen resetten Sie zunächst den Zufallsgenerator von R. Geben Sie hierzu den folgenden Befehl ein: set.seed(1)
- Die erste Stichprobe besteht aus 100 standardnormalverteilten Zufallszahlen und wird als X1 bezeichnet.
- Die Stichprobe X1 wird erzeugt mittels des folgenden R-Befehls: X1 <- rnorm(100)
- Die zweite Stichprobe besteht aus 100 Zufallszahlen aus einer t-Verteilung mit 3 Freiheitsgraden und wird als X2 bezeichnet
- Erzeugen Sie die Stichprobe X2 durch Eingabe des folgenden R-Befehls: X2 <- rt(100,3)
Wir wählen hier als Beispiel die t-Verteilung, da diese Verteilung ein gutes Beispiel für eine Verteilung ist, die sich zwar von der Normalverteilung unterscheidet, jedoch manchmal fälschlicherweise als Normalverteilung erkannt wird.
Betrachten Sie das folgende Schaubild, in dem die Dichtefunktionen der Normalverteilung sowie der t-Verteilung mit 3 Freiheitsgraden dargestellt ist:
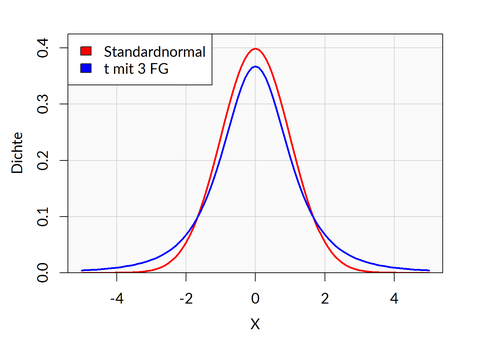
Es ist zu sehen, dass die beiden Verteilungen einige Gemeinsamkeiten aufweisen: Beide sind symmetrisch und haben nur einen Hochpunkt. Ein wesentlicher Unterschied besteht jedoch darin, dass die t-Verteilung an den Rändern links uns rechts jeweils deutlich über der Normalverteilung liegt. Dies bewirkt, dass bei einer t-Verteilung sehr viel häufiger Ausreißer auftreten als bei einer Normalverteilung.
Kommen wir nun zurück zu unseren zuvor erstellten Stichproben X1 und X2. Wir wenden auf beide Stichproben jeweils den Shapiro-Wilk-Test und den Kolmogorov-Smirnov-Test mit R an. Hierzu werden wir die folgenden 4 Befehle verwendet.
shapiro.test(X1)
ks.test(X1,"pnorm")
shapiro.test(X2)
ks.test(X2,"pnorm")
Nach Eingabe aller Befehle erhalten Sie in R den folgenden Output:

Achten Sie in jedem der einzelnen Outputs auf die Zahl p-value. Dies ist der p-Wert des Tests, und anhand des p-Werts wird die Entscheidung getroffen, ob eine Normalverteilung vorliegt.
- Der mit R berechnete Shapiro-Wilk-Test zeigt für die Stichprobe X1 einen p-Wert von p=0.9876. Somit entscheidet der Test, dass eine Normalverteilung vorliegt. Diese Testentscheidung ist korrekt, denn es handelt sich bei X1 tatsächlich um normalverteilte Zahlen.
- Der Kolmogorov-Smirnov-Test, der mit R berechnet wurde, zeigt für die Stichprobe X1 einen p-Wert von p=0.3317. Somit entscheidet auch der Kolmogorov-Smirnov-Test korrekterweise, dass hier eine Normalverteilung vorliegt.
- Was die Stichprobe X2 angeht, so zeigt der Shapiro-Wilk-Test einen p-Wert von p=0.03656. Da dieser Wert kleiner als 0.05 ist, entscheidet der Test, dass keine Normalverteilung vorliegt. Diese Entscheidung ist korrekt, denn die Stichprobe stammt aus einer t-Verteilung.
- Der Kolmogorov-Smirnov-Test hingegen zeigt für die Stichprobe X2 einen p-Wert von p=0.4889. Dieser Wert ist größer als 0.05, somit entscheidet der Test dass diese Stichprobe normalverteilt ist. Hier trifft der Kolmogorov-Smirnov-Test also eine falsche Entscheidung.
Als Fazit dieser Analyse können Sie somit mitnehmen, dass der Shapiro-Wilk-Test eine höhere Teststärke aufweist, d.h. dass er besser darin ist, Abweichungen von der Normalverteilung zu erkennen als der Kolmogorov-Smirnov-Test.
