Ein Histogramm ist eine Graphik zur Darstellung der Verteilung einer Variable. Ein Histogramm können Sie z.B. immer dann erstellen, wenn Sie sich eine Variable "einfach mal ansehen" möchten, ohne dafür gleich eine statistische Beratung konsultieren zu müssen.

Um ein Histogramm zu erstellen, benötigen wir zunächst ein paar Daten. Wir simulieren uns daher 500 Zahlen aus einer Standardnormalverteilung. Hierzu geben Sie den folgenden Befehl in die R-Konsole ein:

x <- rnorm(500)

Wir erstellen nun zunächst ein einfaches Histogramm, welches wir danach etwas ausschmücken werden. Das grundlegende Histogramm wird mittels des R-Befehls hist() erstellt, der auf die Datenreihe x angewandt wird. Geben Sie hierzu den folgenden Befehl in die R-Konsole ein:

hist(x) 

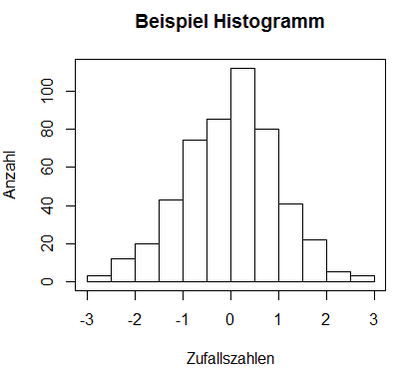
Hierdurch erhält man die folgende Graphik:

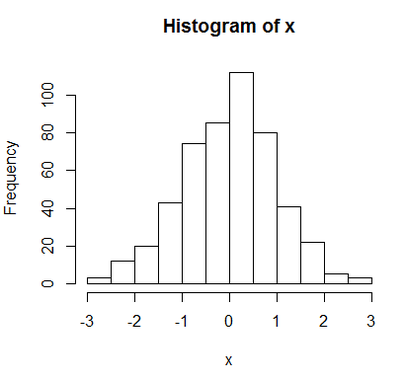
Man erkennt, dass das Histogramm in seiner Basis-Version etwas schlicht und farblos erscheint. Wir möchten Ihnen nun verschiedene Möglichkeiten zur Verschönerung eines solchen Histogrammes präsentieren, wie z.B. mit individuellen Achsenbeschriftungen und einem Titel.

Im ersten Schritt möchten wir die Überschrift sowie die Achsenbeschriftungen ändern und einen Kasten um die Graphik zeichnen. Hierzu geben Sie in die R-Konsole die folgenden Befehle ein:

hist(x,main="Beispiel Histogramm",

xlab="Zufallszahlen",ylab="Anzahl")

box()

Der Parameter main erzeugt die Überschrift des Plots und mit den Parametern xlab und ylab erzeugen wir die Beschriftungen der beiden Achsen. Hierbei steht xlab für die Beschriftung der waagerechten Achse und ylab für die Beschriftung der senkrechten Achse. Die Beschriftungen sind frei wählbar. Um den Kasten zu erstellen, muss nach der Erstellung des Histogrammes der Befehl box() eingegeben werden. Die resultierende Abbildung ist in folgender Graphik dargestellt:

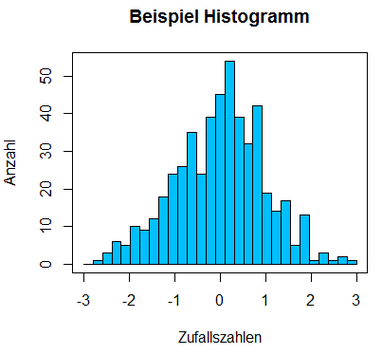
Lassen Sie uns nun ein Histogramm erstellen, das eine blaue Farbe hat und darüber hinaus eine feinere Aufteilung der x-Achse in Intervalle aufweist. Wir wählen hier eine Anzahl von 30 Intervallen. Wir nehmen als Vorlage den Code des letzten Beispiels und erweitern ihn folgendermaßen:

hist(x,main="Beispiel Histogramm",

xlab="Zufallszahlen",ylab="Anzahl",

col="deepskyblue",

breaks=seq(-3,3,length=30))

box()

Die Farbe des Histogrammes wird durch den Parameter col festgelegt, wobei hier die Farbe deepskyblue gewählt wurde. Die Anzahl der Intervalle haben wir mit der Option breaks festgelegt. Das Argument seq(-3,3,length=30) legt fest, dass die Intervalle bei -3 starten und bei 3 enden bei insgesamt 30 Schritten. Die so erzeugte Graphik sieht folgendermaßen aus:

Als Letztes erstellen wir ein Histogramm mit eingezeichneter Dichtefunktion einer Normalverteilung. Eine solche Graphik wird häufig gezeichnet um zu überprüfen, ob Daten mit der Normalverteilung übereinstimmen. Wir geben zu diesem Zweck den folgenden Code ein:

hist(x,main="Beispiel Histogramm",

xlab="Zufallszahlen",

ylab="Wahrscheinlichkeitsdichte",

col="deepskyblue",

breaks=seq(-3,3,length=30), 

freq=FALSE)

m <- mean(x)

s <-  sd(x)

curve(dnorm(x,m,s),add=TRUE,lwd=3)

box()

Mit diesem Code wird die folgende Graphik erzeugt:

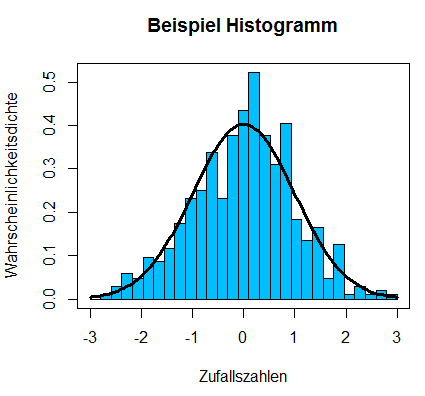
Die Befehle, die im Vergleich zum vorigen Schritt dazugekommen sind, bewirken das Folgende: Die Option freq=FALSE bewirkt, dass auf der y-Achse nicht mehr die Anzahl an Werten, sondern die sogenannte Wahrscheinlichkeitsdichte abgebildet ist. Dementsprechend wurde die y-Achsenbeschriftung mit dem Befehl ylab="Wahrscheinlichkeitsdichte" angepasst. Durch die Verwendung der Option freq=FALSE werden die Höhen der Balken des Histogramms so normiert, dass die Fläche aller Balken zusammen in Summe 1 ergibt. Dies ist notwendig, um die Kurve der Normalverteilung einzeichnen zu können, da bei einer Wahrscheinlichkeitsdichte die Fläche unter der Kurve immer genau 1 betragen muss.

Weiterhin werden mit mean() und sd() der Mittelwert und die Standardabweichung der Werte von x berechnet. Diese werden dann als Parameter der Wahrscheinlichkeitsdichte verwendet, welche mit der Funktion dnorm gezeichnet wird. Der Teil dnorm(x,m,s) in obigem Befehl steht für die Dichte einer Normalverteilung, wobei der Mittelwert und die Standardabweichung aus den Werten der Variable x berechnet werden.

Ein solches Histogramm eignet sich sehr gut, um zu prüfen ob eine metrische Variable eine Normalverteilung aufweist. Das erkennt man daran, wie gut die Balken des Histogrammes mit der eingezeichneten Normalverteilungskurve übereinstimmen. In unserem Beispiel sehen Sie in der zuletzt erzeugten Graphik, dass die Balken des Histogrammes fast die selbe Form aufweisen, wie die Kurve der Normalverteilung. Die Graphik deutet somit darauf hin, dass die Variable x normalverteilt ist, was natürlich daran liegt, dass x in diesem Beispiel eine künstlich erzeugte normalverteilte Variable war, die mit dem Befehl rnorm() erzeugt wurde.

Benötigen Sie weitere Informationen über R? Informieren Sie sich auf unserer Startseite über unser Angebot der statistischen Beratung.